Perpetual student. Interested in Maths, Computer Science and Machine Learning.
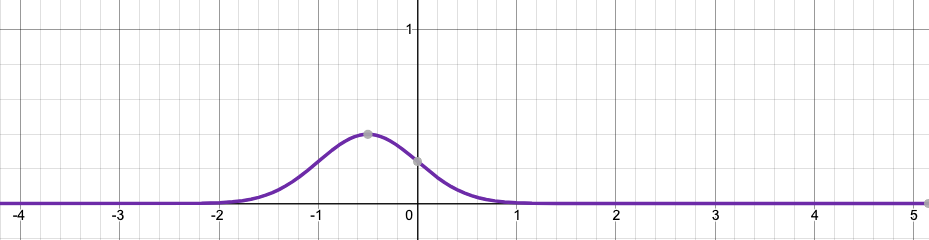
Given the PDF of a random variable $X$, how do you get the PDF of a derived random variable $2X+1$? It is very simple. The probability of any value $x$ will now be the probability of $2x+1$. Therefore, the entire PDF is stretched (horizontally) to twice its size, and then translated horizontally to the right by $1$ unit.
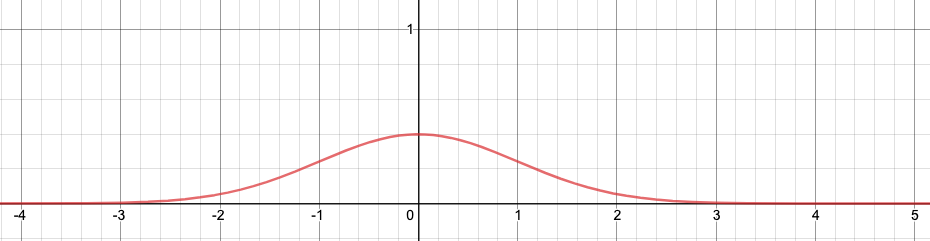
Notice that the area under the graph is constant (total probability over $\mathbb{R}$ is $1$). Therefore, if the graph is stretched horizontally, then it will be shrinked vertically.
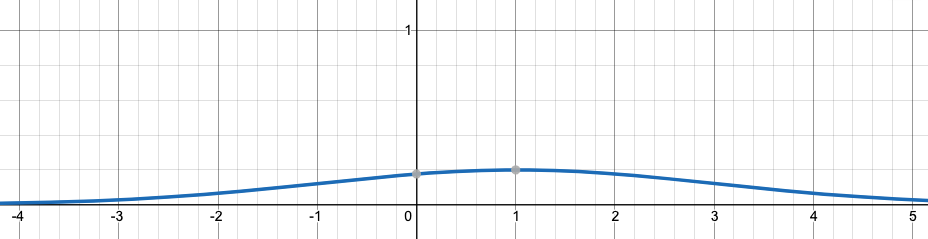
Now let us talk about general functions. If we are given the graph of $f(x)$, how do we derive the graph of $g(x) = f(2x+1)$? Do we follow the same procedure that we used to plot the PDF of a linear transformation of a random variable? Notice here that (unlike transformation of random variable) the new value mapped to $2x+1$ by $g$ isn’t equal to the value that was mapped to $x$ previously by $f$. Rather $x$ is now assigned the value that was assigned to $2x+1$ previously. If we refer to $2x+1$ as $x_{prev}$, then
\[\begin{align} &2x + 1 = x_{prev}\\ \implies &x = \frac{x_{prev}-1}{2} \\ \textrm{and } &g(\frac{x_{prev}-1}{2}) = f(x_{prev}) \end{align}\]The value that was initially assigned to $x_{prev}$ by $f$ is now assigned to $\frac{x_{prev}-1}{2}$ by $g$. Thus, to derive the graph of $g$, we first translate the graph of $f$ to the left by $1$ unit and then shrink it to half.