
Perpetual student. Interested in Maths, Computer Science and Machine Learning.
Till now we have only worked with square matrices and linear systems with as many equations as the number of unknowns. Now we step into the realm of non-square matrices. These notes are majorly derived from MIT OCW 18.06 Series.
We have already studied column spaces and null spaces. Following is some additional commentary on subspaces, column spaces and null-spaces:
For a matrix $A \in \mathbb{R}^{m\times n}$, the column space of $A$ (denoted by $\bt{R}(A)$) is a subset of $\mathbb{R}^m.$
For a matrix $A \in \mathbb{R}^{m\times n}$, the null space of $A$ (denoted by $\bt{N}(A)$) is a subset of $\mathbb{R}^n.$
All the basis sets of a subspace have the same number of vectors. The number of vectors in the basis of a subspace is known as the dimension of the subspace. Proof $\mid$ Khan Academy
If a subspace of $\mathbb{R}^m$ has dimension $m$, then that subspace is itself $\mathbb{R}^m$.
The maximum dimension of any subspace of $\mathbb{R}^m$ is $m$. Or in other words, if $\bt{v_1}, \bt{v_2}, \cdots, \bt{v_n} \in \mathbb{R}^m$, then
Let us prove that if $\bt{V}$ is a subspace of $\mathbb{R}^n$ with dimension $n$, then $\bt{V} = \mathbb{R}^n$. If $\bt{V} \subsetneqq \mathbb{R}^n$, then we need to add a few vector from basis($\mathbb{R}^n$) to basis($\bt{V}$), in order to span the full space of $\mathbb{R}^n$. However the basis that we get in this way will have more than $n$ independent vectors. Comment 3 says that all the different basis sets of a vector space have the same number of vectors. Hence, $\bt{V} = \mathbb{R}^n$. This also proves that there can be atmost $n$ independent vectors in $\mathbb{R}^n$.
Matrix Rank: The rank of $A \in \mathbb{R}^{m\times n}$, denoted by rank$(A)$, is the maximum number of linearly indepedent columns of $A$.
We already saw that if ${\bt{v_1}, \bt{v_2}, \cdots, \bt{v_k}} \subset \mathbb{R}^m$ are linearly independent, then $m\geq k$. So rank$(A)$ $\leq m$. Also, since $A$ only has $n$ columns, rank$(A)$ $\leq n$. Therefore,
\[\textrm{rank}(A) \leq \textrm{min}(m, n)\]If rank$(A)$ = min$(m, n)$, then $A$ is called a full-rank matrix.

We have a definition for the column space and the nullspace of a matrix, but how do we compute these subspaces? How do we know if some vector $\bt{b}$ belongs to $\bt{R}(A)$? And if yes, how do we find a $\bt{x}$ for which $A\bt{x} = \bt{b}$? How do we find the $\bt{x}$(s) for which $A\bt{x} = \bt{0}$?
First let us reiterate what we have learnt till now. We studied the case where $A$ is a square matrix. We initially talked about the case where the diagonal elements in the upper triangular form are non-zero (with or without row permutations). In this case, the nullspace is just ${\bt{0}}$. The column space is $\mathbb{R}^n$ and the solution to $A\bt{x} = \bt{b}$ is given by $\bt{x} = A^{-1}\bt{b}$. Then we talked about the case where the $i^{th}$ diagonal element is zero. In this scenario, if $i^{th}$ and $(i+1)^{th}$ equations reduce to the same thing, then there are infinitely many solutions possible; if not, then there are zero solutions. Either ways $A$ is non-invertible if diagonal elements are $0$. The diagonal elements are responsible for satisfying their respective row equations. If a diagonal element in the upper triangular form is $0$, then the corresponding variable can take any value freely (in case some solution does exist). Therefore, these diagonal elements of $U$ are called pivots (as they are pivotal in deciding the value of the corresponding variable).
Now we try to generalize the above-mentioned technique to non-square non-invertible matrices. First we discuss how to find the null-space and then we focus on the column space.
First, get $A$ in Row-Echelon Form. A matrix in Row-Echelon Form looks like a stair-case. Take $(1,1)$ as the pivot element. Reduce all the elements below the pivot element (in the same column) to zero. Then move diagonally to the next column & next row. If all the elements in the next column (in and below the next row) are zero then move to the next column (same row). Continue in the same fashion till you find an element which is non-zero. This will be a pivot element. Again try to make all elements under this pivot element to be equal to zero. If row permutations can get you a non-zero element in the current position, then do permute the current row with any row below it.
The pivots are the first non-zero elements in their respective rows. Below each pivot is a column of zeros. Each pivot lies to the right of the pivot in the row above it. Every row in row-echelon form either has a pivot-element or is a row of only zeros. The pivot elements decide the value of the corresponding variables. Hence the name “pivot elements”.
Remember that performing row eliminations on a matrix doesn’t change the null-space of the matrix. This is because applying same row operations on $\bt{0}$, we can only get $\bt{0}$.
The elements below a pivot element are zero in Row-Echelon Form. Now, we can go further and make the elements above the pivot elements also equal to zero (using row eliminations). In Reduced Row Echelon Form, all the elements in the pivot columns (with the exception of pivot itself) are equal to zero.
Let $R$ be the RREF for $A$. If we move all the pivot columns to one side of the matrix, then $R$ can be represented as:
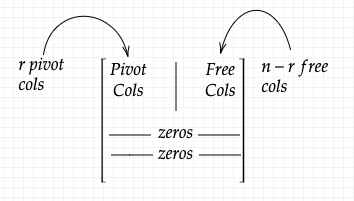
Also,
\[\begin{align} A\bt{x} &= \bt{0}\\ &\big\downarrow &\textrm{eliminations}\\ U\bt{x} &= \bt{0}\\ &\big\downarrow &\textrm{eliminations}\\ R\bt{x} &= \bt{0}\\ \end{align}\]Notice how the definition of pivot element changes from “non-zero diagonal element” in square matrix case, to “first non-zero element in the row” in non-square matrix case. Irrespective of the definition, pivot elements are the only non-zero elements in their respective columns in reduced-row echelon form for both square and non-square matrices.
Removing the zero rows and expressing pivot columns as Identity Matrix, we get:
\[\begin{align} \mat{I & F}\mat{\bt{x_{pivot}}\\\bt{x_{free}}} &= \bt{0} \\ \bt{x_{pivot}} &= -F\bt{x_{free}} \end{align}\]Basically each non-zero linear equation above gives directly the value of a pivot variable if we substitute arbitrary values for free variables. All \(\bt{x} = \mat{\bt{x_{pivot}}\\\bt{x_{free}}}\) that satisfy the above equation fall in the null space of $A$. The subspace \(\{\bt{x} \in \mathbb{R}^n\;\mid\;A\bt{x} = \bt{0}\}\) has dimension equal to the number of free variables. Why? Because though $\bt{x}$ in a $n$-D vector, only $n-r$ of its co-ordinates can change freely. So $\bt{x}$ has to lie on a $n-r$ dimensional hyperplane inside $\mathbb{R}^n$. Need a more rigourous proof? Proof $\mid$ Khan Academy
\[\textrm{dim}(\bt{N}(A)) = n - r\]We have already proved a very important property about the dimension of the column space of $A$:
\[\textrm{dim}(\bt{R}(A)) \leq \min(m, n)\]We also saw that the row reduced echelon form of $A$ is of the following form:
\[R = \mat{ \begin{array}{c|c} I & F \\ \hline \bt{0} & \bt{0} \\ \end{array}}\]All the columns of \(\mat{F \\ \bt{0}}\) can be obtained as linear combinations of \(\mat{I \\ \bt{0}}\). Also all vectors of \(\mat{I \\ \bt{0}}\) are linearly independent. Thus \(\mat{I \\ \bt{0}}\) spans the column space of $R$. Thus,
\[\textrm{rank}(R) = r\]But remember that $R$ and $A$ have different column-spaces (inspite of having the same null space). Therefore the argument above doesn’t prove that $\textrm{rank}(A) = r$. How do we prove that $\textrm{rank}(A) = \textrm{rank}(R) = r$? We don’t. KhanAcademy does!
One major takeaway from this discussion of pivot variables and free variables is a formal proof for the following property: \(\textrm{dim}(\bt{R}(A)) + \textrm{dim}(\bt{N}(A)) = r + (n-r) = n\) where $A \in \mathbb{R}^{m\times n}$.
It is easy to catch the geometric intuition for this property. Roughly speaking, the column vectors in $A$ either contribute to the column space (range) of $A$ or map to $\bt{0}$. All dimensions are accounted for.
To solve $A\bt{x} = \bt{b}$, we use the augmented matrix \(\mat{A \; \mid \; \bt{b}}\) and do the same procedure that we did to solve $A\bt{x} = \bt{0}$.
Suppose $\bt{x_b}$ is a solution for $A\bt{x} = \bt{b}$ and $\bt{x_n}\in \bt{N}(A)$. Then, \(A(\bt{x_b} + \bt{x_n}) = \bt{b}\) and therefore $\bt{x_b} + \bt{x_n}$ is also a solution to $A\bt{x} = \bt{b}$.
Let $A$ be a $m\times n$ matrix.
Case I: $r = n$
$A$ is said to be a full-column rank matrix if $\textrm{rank}(A) = r = n$. This is possible only when $n \leq m$. In this case, there are no free variables/columns. \(\bt{N}(A) = \{\bt{0}\}\) Therefore $A\bt{x} = \bt{b}$ can have atmost one solution.
Case II: $r = m$
$A$ is said to be full-row rank matrix if $\textrm{rank}(A) = r = m$. This is possible only when $m \leq n$. In this case, the columns of $A$ span the entire $\mathbb{R}^m$ and there is a solution for all $A\bt{x} = \bt{b}$, where $\bt{b} \in \mathbb{R}^m$.
These notes by Prof Laurent Lessard also give a very clear explanation of how to solve $A\bt{x} = \bt{0}$ and $A\bt{x} = \bt{b}$. Finally, go over the Four Fundamental Subspaces as explained in this note.